
The total mechanical energy of the system can now be calculated The kinetic energy of the system is given by The potential energy of the system is givenbyįigure 15.1. The total mechanical energy of the simple harmonic oscillator consistof potential and kinetic energy.

The period T of the oscillation is given by It willoscillate with an angular frequency given by

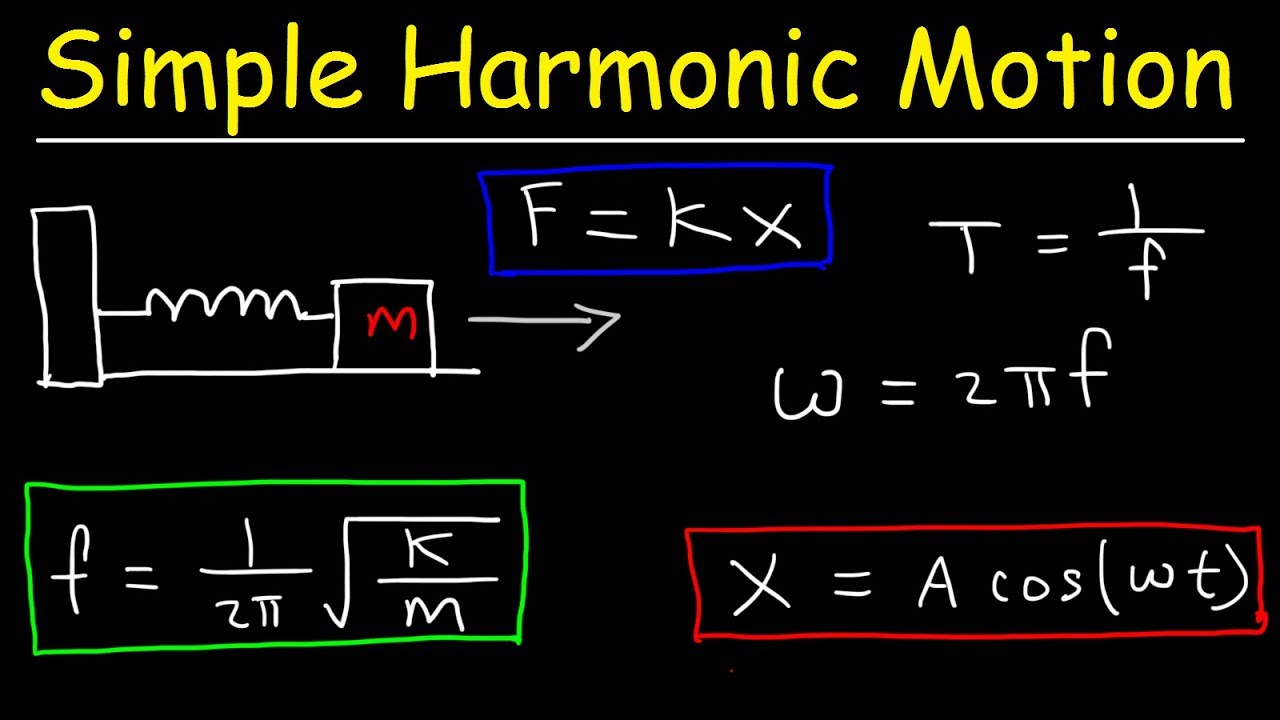
The system shown in Figure 15.1 forms a simple harmonic oscillator. " Simple harmonic motion is the motion executed by a particle ofmass m, subject to a force F that is proportional to the displacement of theparticle, but opposite in sign. This equation of force is similar to the force exerted by a spring(Hooke's law)Ĭomparing these last two equations we conclude that The force acting on the mass can be calculated usingNewton's second law This shows that the acceleration is proportional to the displacement,but opposite in sign. Using the expression forx(t), the expression for a(t) can be rewritten as The positive quantity 2 x m is the acceleration amplitude a m. The acceleration of an object carrying out simple harmonic motionis given by Thismeans that the velocity is greatest when the displacement is zero and viceversa. The positive quantity x m is called the velocity amplitude and is the maximum velocity of the object.Note that the phase of the velocity and displacement differ by 90deg. The velocity of an object carrying out simple harmonic motion can becalculated easily The period T and the frequency are related as follows The symbol for frequency is and its unit is the Hertz (Hz): The number of oscillations carried out per second is called the frequency of the oscillation. Therefore, the displacement x(t) must return to itsinitial value after one period The period T of the motion is defined as the time required tocomplete one oscillation. The angular frequency is a characteristic of the system, and does not depend on the initialconditions. The phase constant isdetermined by the initial conditions. The time-varyingquantity (t + ) is called the phase of the motionand is called the phase constant.

The quantity x m is called the amplitude of themotion and is the maximum displacement of the mass. Where x m, and are constants, independent oftime. A particle experiences a simple harmonics motion if itsdisplacement from the origin as function of time is given by Any motion that repeats itself at regular intervals is called harmonicmotion.


 0 kommentar(er)
0 kommentar(er)
